Canonical
Logistic Regression for Ordinal Categorical Response Using %CANLOG
Jochem König
Institut für
Medizinsche Biometrie, Epidemiologie und Medizinische Informatik,
Universität des Saarlandes, 66421 Homburg.
jk@med-imbei.uni-saarland.de
1- Notation and models
All models are submodels of multinomial response logistic model:
(1)
The repsonse variable Y is assumed to have m ordered
response categories coded 1,…,m and 
denotes the conditional
probability for category j given a realisation x of the vector X
of explanatory variables. The conditional distribution of the response Y given
the explanatory variables is sometimes referred to as posterior distribution.
2-An
excursion on sampling schemes priors, marginal and class conditional
distributions
If there is an underlying common distribution of Y and X, it can be
decomposed in two ways:
(2)
where f is termed marginal density, fy are class
conditional densities and py are priors. Three types of sampling may
be used for fitting: mixture sampling denotes a sample from the common
distribution of (Y,X); controlled sampling denotes a set of independent
drawings from the collection of posterior distributions, i.e. information on X
may have been used to select subjects for the study; and finally, separate
sampling addresses independent samples from each of the class conditional
distributions.
Under mixture sampling and controlled sampling, posteriors may be
computed from an ML-fit of (1) via
(3)
prior estimates may be obtained as sample proportions under mixture
sampling and are unknown under controlled sampling.
Under seperate sampling, (1) a formal ML-fit of
(4)
to the data yields ML estimates of density ratios via
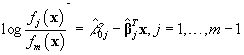, (5)
where nj denote sample sizes. Assuming equal priors, (5) may
be interpretated as an equation for posterior ratios like (1) (but note that an
offset was introduced during fitting and than removed). Adding any set of
logits 
of priors known form
some other source on both sides of (5) makes (5) to an equation of type (1)
that may be used to compute posteriors via (3). Similarly results from mixture
sampling may be transferred to a situtaion with the same class conditional
distribution, but different priors (and consequently different marginal and
posterior distribution) by adding constants to equation (1).
3- Models continued
Parametrization (1) is referred to as last category coding. After
reversing signs of regression coefficients it is identical to that used in proc
catmod.
In parallel, adjacent coding, an equivalent parametrization is
used in the macro:
(6)
All specific models may be presented as a meta model for the set of
vectors of regression coefficients. Where conveniant, 
is defined.
For instance, Andersons stereo type model uses last category coding:
(7)
An ordinal relationship is stated once 
holds. More
precisely, the constraints establish a stochastically monotone relationship
between a single linear predictor 
and the response
variable. (Anderson 1984). Ties between successive f parameters indicate indistinguishable
categories
Equivalently, in adjacent coding
(8)
here order constraints are formulated as 
. And indistinguishability between categories j and j+1 may
be stated as 
.
Now, a class of models called partially ordinal logistic model is
introduced, that contains models more restrictive than (1/6) and more general
than (7/8) (see Feldmann,König). These models put collinearity constraints on
some but not all of the regression vectors (8):
(9)
for some given subset of indices
. Any such set of starting categories of collinear sequences fully
specifies a partially ordinal logistic model. Note, that (6) and (8) are
included as special cases r=m-1 and r=1, respectively.
Example: m=7, r=3, {j1,..,jr+1}={1,
4, 5, 7}; then 1-2-3-4, 4-5 and 5-6-7 are joint by collinear regression vectors
that are multiples of 
, repsectively. The entries of 
have to be
interpreted as average unit log odd ratio between adjacent categories among the
set {1,2,3,4} of categories, where as the entries of 
are still specific
unit odds ratios between categories j and j+1 as in model (6).
Each of the models (8) and (9) may be further restricted by fixing the
tau parameters as known constants. For the fixed scales models of %CANLOG, all
tau are set to one:
(10)
Anderson also considers models where
all regression vectors of (1) (or equivalently of (6) are assumed to lie in an
unknown d-dimensional linear subspace, e.g. in adjacent coding:
(11)
Note that any model (9) spans a subspace of dimension at most r and is
nested in the model (11) with d=r.
The data generated choice between models of type (11) was termed canonical
logistic regression by McCullagh (in the discussion of Anderson 1984). Here
any data generated selection between models (9,10,11) is termed canonical
logistic regression.
5-Specifications
The macro-parameters of %CANLOG are as follows
%macro canlog(y,xliste,
numvar=1,
data=_last_,
crit=0.0001,
id=,
partial=,
reverse=1,
priors=equal,
out=outpred,outb=outpredb,
outest=outest,
outestb=outestb,
);
macro parameters of %CANLOG
|
Parameter |
Explanation |
|
y |
response
variable coded 1,2,...,m |
|
xliste |
list of explanatory
variables |
|
id |
list of
numerical identification variables (optional) |
|
data |
input
data set (training sample) |
|
partial |
sequence
of indices specifying a partially collinear model: e.g.let m=12. then 1 2 6 7 8 11 specifies a model where coefficient vectors 2-3-4-5
and 8-9-10 are collinear (adjacent coding) |
|
priors |
set of q
priors if different from sample sizes (q= number of categories minus 1). key
word equal produces constant priors |
|
reverse=1 |
reversal
of sign for all variables, leads to positive coefficients if higher values of
explanatory variable are associated with a trend towards higher response
values. option does not affect contents of outestb which is organized to
conform with proc catmod. |
|
outb |
name of
output dataset containing one row for each row of data |
|
out |
name of
output dataset containing q rows for each rows of data |
|
outest |
name of
output dataset containing parameter estimates |
|
outestb |
name of output
dataset containing parameter estimates format compatible to that of proc
catmod |
5-Models Fitted
%CANLOG fits by default the full multinomial model and the
onedimensional stereotype model with equidistant fixed scales and with estimated
scale parameters. Parameters are estimated in the adjacent coding scheme and in
the last category coding. Partially ordinal models are fitted if specified via
macro parameter partial: one with estimated scale parameters and one with fixed
constant scale parameters.
models fitted by %CANLOG
|
model
idenfying string |
Explanation |
|
glogitm |
multinomial
model |
|
glogit1e |
stereotype
model 1-dimensional, estimated scale parameters |
|
glogit1f |
stereotype
model 1-dimensional, fixed constant scale parameters |
|
pa(&partial) |
partially
ordinal model, estimated scale parameters |
|
paf(&partial) |
partially
ordinal model, fixed constant scale parameters |
6-Output Datasets
Output dataset &outb
Output dataset &outb contains one row for each row of data.
Output dataset &outb Description of
vaiables
|
Variable
name |
name of
output dataset containing one row for each row of data and the following
variables |
|
y |
response
variable |
|
ybayes |
predicted
category from bayes rule, |
|
y_ml |
predicted
category from maximum likelihood rule i.e. assuming equal priors, |
|
y_lc |
rule
minimzing the Bayesrisk assuming linearly increasing costs of
misclassification |
|
y_lce |
same as y_lc,
but assuming equal priors. |
|
y_ex |
expected
value of y as computed from posteriors rounded to the nearest integer |
|
post1,post2,.. |
variables
for posteriors (priors as proportions in data set) and |
Output dataset &out
Output dataset &out
contains q:=m-1 rows for each rows of data
Output dataset &out: Description of
vaiables
|
Variable
name |
name of
output dataset containing one row for each row of data and the following
variables |
|
&id |
idvariable
(optional) |
|
y |
response
variable as row indicator |
|
xbeta |
linear
predictor |
|
post |
posterior
for category given by y |
6-Printed Output
For each model fitted parameters estimated and standard errors are
given.